Розв'язування систем показникових рівнянь

Розв'язування  систем показникових рівнянь

Пр.1 Розв'яжемо рівняння

 

Перш за все виконаємо перетворення

 

Зробимо заміну 

Отримуємо:   

Повертаючись до заміни, маємо:   тоді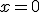 

або   коренів не має.

Відповідь:  0.

Заміна і обернена заміна - це рівносильні перетворення заданого рівняння, але при розв'язуванні одержаного дробового рівняння слід подбати про те, щоб не отримати сторонніх коренів (для цього, наприклад, досить врахувати, що t > 0).

У Пр.1

• позбуваємося числових доданків у показниках степенів;
• потім зводимо всі степені (із змінною в показнику) до однієї основи 5;
• виконуємо заміну  і розв'язуємо одержане рівняння;
• здійснюємо обернену заміну і розв'язуємо одержані найпростіші показникові рівняння
• а також враховуємо, що всі перетворення були рівносильними.

Пр.2 Розв'яжемо рівняння 

 

Відповідь: 2.

Позбуваємося числових доданків у показниках степенів, переносимо всі члени рівняння в один бік і зводимо подібні члени.

Помічаємо, що степені всіх членів одержаного рівняння ( з двома основами 2 і 3) однакові - 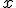, отже, це рівняння однорідне. Його можна розв'язати діленням обох частин на найвищий степінь одного з видів виразу із змінною - або на  , або на 

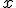Враховуючи, що  при всіх значеннях , у результаті ділення на отримуємо рівняння, рівносильне попередньому (а отже, і заданому).

При розв'язуванні систем рівнянь, що містять показникові функції, найчастіше використовуються традиційні методи розв'язування систем рівнянь: метод підстановки і метод заміни змінних.

Пр.3 Розв'яжемо систему рівнянь:

Нехай  Розв'яжемо окремо друге рівняння системи:

 

Повертаючись до заміни маємо:

  тоді   або     тоді 

Знаходимо відповідні значення  

якщо    то 

якщо    то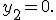 

Відповідь: (0; 1); (1; 0).

Пр.4  Розв'яжемо систему рівнянь:

 

Введемо заміну  Тоді система прийме вид:

З другого рівняння системи маємо: 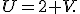 Тоді перше рівняння системи прийме вигляд   Звідки    тоді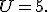   

Повертаючись до заміни маємо:

  тоді    отже,   

  тоді    отже,   

Відповідь. (2;2).