Способи розв'язання показникових нерівностей

Нерівності виду a^f(x) ≥ a^g(x), a^f(x) > a^g(x) , де a > 0, a ≠ 1.

Метод розв’язування нерівності а^х ≥ b можна узагальнити для нерівностей виду a^f(x) ≥ a^g(x), a^f(x) > a^g(x) , де a > 0, a ≠ 1. Подамо метод розв’язування нерівності у вигляді таблиці.

af(x) ≥ ag(x)
0 < а < 1	а > 1
Знак нерівності змінюється на протилежнийf(х) ≤ g(x)	Знак нерівності не змінюється f(х) ≥ g(x)

Аналогічно розв’язується нерівність виду a^f(x) > a^g(x).

Приклад. Розв’яжіть нерівності: 

Розв’язання.

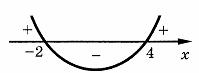
2) Оскільки 0 < ½ < 1, то маємо  Розв’язавши цю нерівність,маємо х ≤ -1 або х ≥ 4 (мал. 48).



Способи розв'язання показникових нерівностей

Пр.1 Розв'язати нерівність:    

Запишемо праву частину нерівності як степінь числа 0,6: 

Оскільки , то при переході від степенів до показників знак нерівності змінюється на протилежний (одержуємо нерівність, рівносильну заданій).

Для розв'язування одержаної квадратної нерівності використаємо графічну ілюстрацію або "метод інтервалів".

Відповідь. 

Пр.2 Розв'язати нерівність:    

Оскільки рівносильні перетворення нерівностей виконуються на ОДЗ початкової нерівності, то зафіксуємо цю ОДЗ :

Використовуючи властивості степенів отримаємо: 

Нехай 

Отримаємо нерівність  яка рівносильна нерівності 

В одержаній нерівності знаменник додатний, тому цю дробову нерівність можна звести до рівносильної їй квадратної:  Звідки 

Враховуючи, що  маємо 

Повертаючись до заміни, отримаємо:   Тоді 

Функція  є зростаючою, отже,  Враховуючи ОДЗ, одержуємо

Відповідь. 

Пр.3 Розв'язати нерівність:    

Задану нерівність можна розв'язувати або зведенням до алгебраїчної нерівності, або методом інтервалів. Для розв'язування її методом інтервалів використаємо схему, наведену на попередньому уроці.

Розв'яжемо нерівність методом інтервалів. Позначимо 

1. ОДЗ: 

2. Нулі функції: 

  ділимо на  

Заміна   Отримуємо: 

Повертаючись до заміни, отримуємо:    та  

Звідки знаходим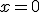о   або  

При знаходженні нулів функції зведемо всі степені до двох основ (2 і 3), щоб одержати однорідне рівняння. Це рівняння розв'язується діленням обох частин на найвищий степінь одного з видів змінних.

3. Відмічаємо нулі функції на ОДЗ, знаходимо знак   у кожному з одержаних проміжків і записуємо розв'язки нерівності 

Відповідь. 

Пр.4 Розв'язати нерівність:    

Задану нестрогу нерівність зручно теж розв'язувати методом інтервалів. Записуючи відповідь, слід враховувати, що у випадку, коли ми розв'язуємо нестрогу нерівність   усі нулі функції   повинні ввійти до відповіді.

Позначимо 

1. ОДЗ:  Тоді   або 

2. Нулі функції: 

 Тоді  або  .

З першого рівняння:  - не входить до ОДЗ, а з другого: 

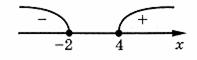
3. Позначимо нулі  на ОДЗ, знаходимо знак  у кожному з проміжків, на які розбивається ОДЗ, і записуємо розв'язки нерівності  

Відповідь.