Логарифм числа.
Властивості логарифмів
ОЗНАЧЕННЯ Логарифмом додатного числа b за основою а ( ) називається показник степеня, до якого треба піднести
) називається показник степеня, до якого треба піднести  , щоб одержати
, щоб одержати 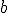 і позначається
і позначається  .
.
Пр.  оскільки
оскільки 
Десятковий логарифм - це логарифм за основою 10
| |
| |
Пр.  оскільки
оскільки 
Безпосередньо з означення логарифма слідує рівність 
 , яка носить назву основна логарифмічна тотожність.
, яка носить назву основна логарифмічна тотожність.
ВЛАСТИВОСТІ ЛОГАРИФМІВ
1.  Логарифм одиниці за будь якою основою дорівнює нулю.
Логарифм одиниці за будь якою основою дорівнює нулю.
2. 
3. =\log_a%20x+\log_a%20y,%20\%20\%20x%3E0,%20\%20y%3E0) Логарифм добутку додатних чисел дорівнює сумі логарифмів множників.
Логарифм добутку додатних чисел дорівнює сумі логарифмів множників.
4. =\log_a%20x-\log_a%20y,%20\%20\%20x%3E0,%20\%20y%3E0) Логарифм частки додатних чисел дорівнює різниці логарифмів діленого і дільника.
Логарифм частки додатних чисел дорівнює різниці логарифмів діленого і дільника.
5.  Логарифм степеня додатного числа дорівнює добутку показника степеня на логарифм основи цього степеня.
Логарифм степеня додатного числа дорівнює добутку показника степеня на логарифм основи цього степеня.
6. Формула переходу до логарифма з іншою основою
Н А С Л І Д К И
Розглянемо приклади на обчислення логарифмів
Пр 1. Обчислити 
Враховуючи означення логарифма, потрібно підібрати такий показник степеня, щоб при піднесенні основи логарифма до цього степеня одержати число, яке стоїть під знаком логарифма.
Пр 2. Обчислити 
Розглянемо ще один спосіб розв'язування показникових рівнянь. Це метод логарифмування обох частин рівняння. Для початку розглянемо найпростіші із таких.
Пр 3. Записати розв'язки найпростіших показникових рівнянь:
а) 
Для будь яких додатних чисел 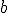 і
і  (
(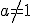 ) рівняння
) рівняння  має єдиний корінь. Показник степеня
має єдиний корінь. Показник степеня 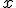 , до якого потрібно піднести основу
, до якого потрібно піднести основу  , щоб одержати
, щоб одержати 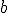 , називається логарифмом
, називається логарифмом 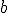 за основою
за основою  , тому
, тому 
Отже, 
б) ^x=10.)
в) 
Пр 4. Виразіть логарифм за основою 3 виразу  (де
(де 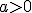 і
і  ) через логарифми за основою 3 чисел
) через логарифми за основою 3 чисел  і
і 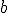 . (Коротко кажуть: «Прологарифмуйте заданий вираз за основою 3».)
. (Коротко кажуть: «Прологарифмуйте заданий вираз за основою 3».)
Спочатку запишемо вирази в чисельнику і знаменнику заданого виразу як степені чисел і букв.
Врахуємо, що логарифм частки  додатних чисел дорівнює різниці логарифмів чисельника і знаменника, а потім те, що логарифм добутку дорівнює сумі логарифмів множників.
додатних чисел дорівнює різниці логарифмів чисельника і знаменника, а потім те, що логарифм добутку дорівнює сумі логарифмів множників.
Після цього ми врахували, що кожен з логарифмів степенів дорівнює добутку показника степеня на логарифм основи цього степеня, а також те, що  .
.
Пр 5. Відомо, що  Виразити
Виразити  через
через  та
та 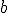 .
.
Спочатку подамо число 700 як добуток степенів заданих чисел 5 і 7 та основи логарифма 2, а потім використаємо властивості логарифмів та підставимо в одержаний вираз значення  та
та 
Пр 6. Прологарифмувати за основою 10 вираз: 
Оскільки логарифми існують тільки для додатних чисел, то ми можемо прологарифмувати заданий вираз тільки у випадку, коли 
З умови не випливає, що в заданому виразі значення  додатні. Тому будемо користуватися узагальненими формулами логарифмування , а також врахуємо, що
додатні. Тому будемо користуватися узагальненими формулами логарифмування , а також врахуємо, що
Якщо  то
то -\lg|c|^2=\lg%20|a|+\lg|b^3|-2\lg%20c=)
ЛОГАРИФМИ
Обчислити логарифмічні вирази:
1.
lоg <1/16> 41/3;
2.
lоg <0,32> (2/5 20,5);
3.
lоg <7> 1/7;
4.
lоg <5>
5;
5.
lоg <3^0,5>9;
6.
lоg <2^0,5>2048;
7.
lоg <1/a2>
(a3)0,5;
8.
lоg <a4>
(a-9)1/7;
9.
lоg <a1/3>(1/(a)2/5);
10.
lоg <1/9>
(27)1/16;
11.
lоg <1/16>(256)1/5;
12.
lоg <1/8>lg<(2)1/3>(4)1/3;
13.
lоg <128>16;
14.
lоg <256>1/32;
15.
lоg <32>4;
16.
lоg <1/16>(1/4);
17.
lоg <1/18>(1/4)7;
18.
lоg <8>(1/2)1/3;
19.
lоg <1/9>(9)1/4;
20.
lоg <9>(1/9)1/8;
21.
lоg <1/7>(1/(49)1/3);
22.
lоg <0,(3)>
(1/(243)1/11);
23.
lоg <25>
(625)1/13;
24.
lоg <64>
(2)1/3;
25.
lоg <25>
(625)1/18;
26.
lоg <(a)1/3>((a)1/4/(a)1/7);
27.
103 lg2;
28.
52log<5>3;
29.
125log<25>16;
30.
640,(6)log
<64>27;
31.
81log<243>32;
32.
7log<7>5;
33.
alog<a>b;
34.
91/4-log<3>4;
35.
5log<25>9;
36.
41/2+log<32>(5)0,5;
Немає коментарів:
Дописати коментар