Розв'язування показникових нерівностей

Розв’язування складніших показникових нерівностей.

При розв’язуванні більш складних показникових нерівностей використовують ті самі прийоми, що й при розв’язуванні рівнянь: спосіб винесення за дужки спільного множника, заміну змінних тощо, намагаючись зводити нерівності до найпростіших.

Приклад 1. Розв’яжіть нерівність: 

Розв’язання. 

Приклад 2. Розв’яжіть нерівність: 

Розв’язання. Заміна  Розв’язуючи цю нерівність, отримаємо t < -1 або t > 3. Повертаємося до змінної х:

 - немає розв’язків.

Отже, розв’язками нерівності є множина (-∞;-1).





Розв'язування показникових нерівностей

Для найпростіших показникових нерівностей застосовують таку схему рівносильних перетворень:

при     знак нерівності зберігається. Приклад: Функція   є зростаючою, отже: Відповідь:	при     знак нерівності змінюється на протилежний. Приклад: Функція   є спадною,отже: Відповідь:
Для розв'язування більш складних показникових нерівностей запропонуємо такий алгоритм: За допомогою рівносильних перетворень задана нерівність зводиться до нерівності відомого виду (квадратної, дробової тощо). Після розв'язування одержаної нерівності приходимо до найпростіших показникових нерівностей.	Заміна   дає нерівність  розв'язки якої  та  Повертаючись до заміни, маємо:  - коренів не має        та , звідки     тобто  Відповідь:
Застосовуємо загальний метод інтервалів, зводячи задану нерівність до виду і використовуючи схему: 1. Знайти ОДЗ. 2. Знайти нулі f (x). 3. Відмітити нулі функції на ОДЗ. і знайти знак f (x) у кожному з проміжків, на які розбивається ОДЗ. 4. Записати відповідь, враховуючи знак нерівності.	Розв'яжемо нерівність методом інтервалів. Задана нерівність рівносильна нерівності  Позначимо   ОДЗ:  Нулі функції: . Оскільки  є зростаючою функцією ( як сума двох зростаючих), то значення 0, вона набуває тільки в одній точці з області визначення. Це . Нулі функції наносимо на числову пряму і знаходимо знак функції на кожному з них і записуємо розв'язки нерівності

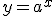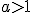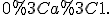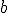Розв'язування найпростіших показникових нерівностей виду  (або , де ) ґрунтується на властивостях функції  яка зростає при  і спадає при  Наприклад, щоб знайти розв'язки нерівності  при  досить подати  у вигляді  Одержуємо нерівність

( 1 )

При 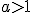 функція  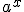зростає, отже, більшому значенню функції відповідає більше значення аргументу, тому з нерівності (1) одержуємо (знак цієї нерівності збігається із знаком нерівності (1)).

При 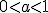 функція  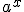 спадає, отже, більшому значенню функції відповідає менше значення аргументу, тому з нерівності (1) одержуємо  (знак цієї нерівності протилежний знаку нерівності (1)).

Наприклад, щоб розв'язати нерівність  досить подати цю нерівність у вигляді  врахувати, що 5>1 (функція  є зростаючою, отже, при переході до аргументів знак нерівності не змінюється), і записати розв'язки: 

Зауважимо, що розв'язки заданої нерівності можна записувати у вигляді  або у вигляді проміжка  

Аналогічно, щоб розв'язати нерівність  досить подати цю нерівність у вигляді  враховуючи, що функція є спадною, отже, при переході до аргументів знак нерівності змінюється на протилежний, і записати розв'язки: 

Враховуючи, що при будь яких додатних значеннях  а значення 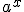 завжди більше нуля, одержуємо, що при нерівність  розв'язків не має, а нерівність  виконується при всіх дійсних значеннях x.

Наприклад, нерівність   не має розв'язків, а розв'язками нерівності  є всі дійсні числа.

Узагальнюючи наведені вище міркування стосовно розв'язування найпростіших показникових нерівностей, відзначимо, що при   знак нерівності зберігається та при   знак нерівності змінюється.

Щоб обґрунтувати рівносильність відповідних нерівностей, досить відзначити, що при 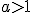 нерівності

( 2 )

( 3 )

можуть бути правильними тільки одночасно, оскільки функція  при 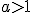 є зростаючою і більшому значенню функції відповідає більше значення аргументу (і навпаки: більшому значенню аргументу відповідає більше значення функції). Отже, усі розв'язки нерівності (2) (які перетворюють її на правильну числову нерівність) будуть і розв'язками нерівності (3), та навпаки: усі розв'язки нерівності (3) будуть розв'язками нерівності (2). А це й означає, що нерівності (2) і (3) є рівносильними.

Аналогічно обґрунтовується рівносильність нерівностей у випадку, коли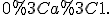  

Зауважимо, що, аналогічно до розв'язування показникових рівнянь, усі рівносильні перетворення нерівності завжди виконуються на її області допустимих значень (тобто на спільній області визначення для всіх функцій, які входять до запису цієї нерівності). Для показникових нерівностей досить часто областю допустимих значень (ОДЗ) є множина всіх дійсних чисел. У цих випадках, як правило, ОДЗ явно не знаходять і не записують до розв'язання нерівності. Але якщо в процесі розв'язування показникової нерівності рівносильні перетворення виконуються не на всій множині дійсних чисел, то в цьому випадку доводиться згадувати про ОДЗ.