Розв'язування складних показникових рівнянь

Розв'язування складних

показникових рівнянь

Зведення показникових рівнянь до найпростіших способом винесення спільного множника за дужки.

Цей спосіб можна використовувати у випадку, коли рівняння містить кілька виразів виду , де m_i — різні числа. Тоді використовуємо формулу = а^х та виносимо за дужки спільний множник. Після спрощень отримаємо рівняння виду а^х = b.

Приклад. Розв’яжіть рівняння: 

Розв’язання.



Заміна змінних у показникових рівняннях.

Досить часто показникові рівняння можна звести до алгебраїчного за допомогою заміни t =a^f(x), зауважимо, що t > 0.

Приклад 1. Розв’яжіть рівняння: 

Розв’язання. Заміна 4^х = t , t > 0. Тоді  Маємо  — не задовольняє умову t > 0.

Отже, 

Приклад 2. Розв’яжіть рівняння: 

Розв’язання. Заміна  Маємо рівняння  Розв’язавши його, матимемо t₁ = 4; t₂ = -2,5 - не задовольняє умову t > 0. Тоді

Однорідні показникові рівняння.

Рівняння виду  є однорідним показниковим рівнянням другого степеня.

Метод розв’язання такого рівняння полягає в діленні лівої і правої частини на b^2f(х) ≠ 0 (або на а^2f(x) ≠ 0). Тоді маємо

Далі заміна 

Приклад. Розв’яжіть рівняння: 

Розв’язання. Оскільки  то рівняння зводиться до однорідного 

Ділимо ліву і праву частини рівняння на 3^2х ≠ 0.

Маємо 

Заміна  Тоді  Маємо 



Пр.1 Розв'яжемо рівняння

 

Враховуючи, що  зводимо до однієї основи 2:

Зробимо заміну  Отримаємо рівняння

 

Повертаємося до заміни: 

Друге рівняння сукупності коренів немає. Єдиним коренем рівняння є число 1.

Відповідь. 1.

Алгоритм розв'язування рівнянь подібного типу такий:

1. Позбавляємося числових доданків у показниках степенів (використовуючи справа наліво основні формули дій над степенями)

2. Якщо можливо, зводимо всі степені (із змінною в показнику) до однієї основи і виконуємо заміну змінної.

3. Якщо не можна звести до однієї основи, то пробуємо звести всі степені до двох основ так, щоб отримати однорідне рівняння (якерозв'язується діленням обох частин рівняння на найбільший степінь одного з видів змінних).

Пр.2 Розв'язати рівняння:

Зведемо всі степені до двох основ: 2 та 3:

 

Маємо однорідне рівняння ( у всіх членів однаковий сумарний степінь - ). Для його розв'язування поділимо обидві частини на 

 

Нехай  тоді отримуємо рівняння:

 

Повертаємося до заміни :

 

Рівняння  коренів не має.

Відповідь. 0.

В інших випадках переносимо всі члени рівняння в один бік і пробуємо розкласти одержаний вираз на множники або застосовуємо спеціальні прийоми розв'язування, в яких використовуються властивості відповідних функцій.

Пр.3 Розв'язати рівняння:

 

Якщо попарно згрупувати члени в лівій частині рівняння і в кожній парі винести за дужки спільний множник, то отримуємо

Спільний множник виносимо за дужки і отримуємо:

Тоді  або 

Отримуємо два рівняння:

, тоді 

 тоді  

Відповідь. 2; 1.

Для розв'язування більш складних показникових рівнянь (порівняно з тими, які було розглянуто на попередньому уроці) найчастіше використовують заміну змінних. Щоб зорієнтуватися, чи можна ввести заміну змінних у даному показниковому рівнянні, часто буває корисно на початку розв'язу вання позбутися числових доданків у показниках степенів, використовуючи властивості степеня. Наприклад. У рівнянні  замість  записуємо добуток  і одержуємо рівняння рівносильне заданому.

Потім пробуємо всі степені (із змінною в показнику) звести до однієї основи і виконати заміну змінної. Наприклад, у Пр1 степінь з основою 4 можна записати як степінь з основою 2:  і отримати рівняння 

Нагадаємо загальний орієнтир: якщо до рівняння, нерівності або тотожності змінна входить в одному і тому самому вигляді, то зручно відповідний вираз із змінною позначити однією буквою (новою змінною).

Зазначимо, що як використання основних формул дій над степенями, так і використання заміни та оберненої заміни завжди приводить до рівняння, рівносильного даному на його ОДЗ ( у Пр1 - на множині всіх дійсних чисел) через те, що всі вказані перетворення ми можемо виконати і в прямому, і в зворотному напрямках. (Отже, ми завжди зможемо довести, що кожен корінь одного рівняння є коренем другого і навпаки. У тих випадках, коли всі степені (із змінною в показнику) у показниковому рівнянні, яке не зводиться безпосередньо до найпростішого, не вдається звести до однієї основи, слід спробувати звести всі степені до двох основ так, щоб одержати однорідне рівняння.

Наприклад, розглянемо рівняння 

Усі степені в цьому рівнянні можна записати через основи 2 і 3, оскільки

 

Одержуємо рівняння 

Усі одночлени, які стоять у лівій частині цього рівняння, мають степінь  (степінь одночлена  теж дорівнює ).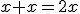

В загальному випадку необхідно діяти так:

Якщо всі члени рівняння, у лівій і правій частинах якого стоять многочлени від двох змінних (або від двох функцій однієї змінної), мають однаковий сумарний степінь, то рівняння називається однорідним.

Розв'язується однорідне рівняння діленням обох його частин на найвищий степінь однієї із змінних.

Отже, рівняння  є однорідним, і його можна розв'язати діленням обох частин або на , або на . Відзначимо, що при всіх значеннях x вирази  і  не дорівнюють нулю. Отже, при діленні на ці вирази не може відбутися втрата коренів (як це могло бути, наприклад, для однорідних тригонометричних рівнянь) і в результаті ділення обох частин рівняння на будь який з цих виразів завжди одержуємо рівняння, рівносильне заданому. Наприклад, якщо розділити обидві частини на  одержуємо   або після скорочення  

В останньому рівнянні всі члени можна подати як степені з однією основою:

  і виконати заміну  

Подальший розв'язок був продемонстрований раніше.

Шукаючи план розв'язування показникового рівняння, потрібно враховувати, що при розв'язуванні деяких із них доцільно перенести всі члени рівняння в один бік і спробувати розкласти одержаний вираз на множники, так як це було продемонстровано при розгляді прикладів.