Поняття показникової функції та її графік
Означення. Показниковою функцією називається функція виду 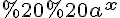 , де
, де 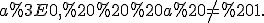
Властивості показникової функції:
1. Область визначення )
2. Область значень: )
3. Функція ні парна, ні непарна.
4. Точки перетину з осями координат: з віссю ординат (0;1) ; з віссю абсцис точок перетину немає.
5. Проміжки зростання і спадання:
функція 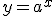 при
при 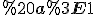 зростає на всій області визначення.
зростає на всій області визначення.
функція 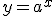 при
при 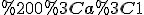 спадає на всій області визначення.
спадає на всій області визначення.
6. Проміжки знакосталості: 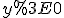 при всіх значеннях аргументу.
при всіх значеннях аргументу.
7. Найбільшого і найменшого значень функція не має.
Обгрунтуємо ці властивості:
Оскільки при 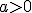 вираз
вираз 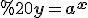 означений при всіх дійсних значеннях x, то областю визначення показникової функції
означений при всіх дійсних значеннях x, то областю визначення показникової функції 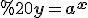 є всі дійсні числа.
є всі дійсні числа.
Функція виду 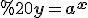 існує й при
існує й при 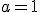 .
.
Тоді 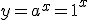 , тобто
, тобто 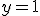 при всіх значеннях
при всіх значеннях 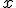 . Але в цьому випадку функція
. Але в цьому випадку функція 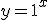 не називається показниковою, оскільки є лінійною функцією
не називається показниковою, оскільки є лінійною функцією 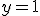 .
.
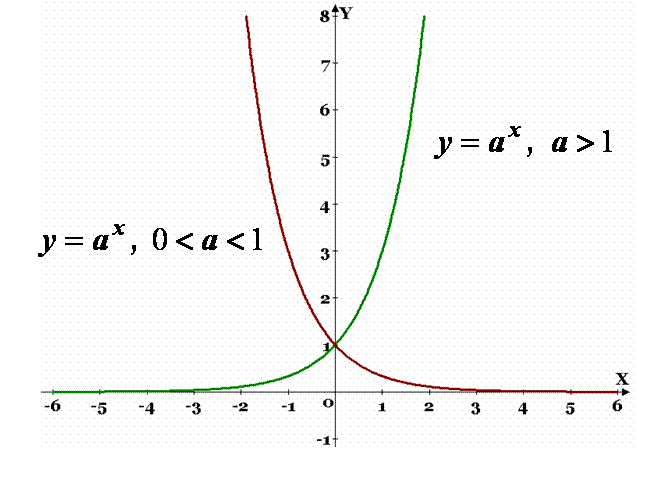
Графік показникової функції називається експонентою.
Областю значень функції 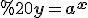 є множина всіх додатних чисел, тобто функція
є множина всіх додатних чисел, тобто функція 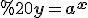 набуває тільки додатних значень, причому будь-яке додатне число є значенням функції, тобто
набуває тільки додатних значень, причому будь-яке додатне число є значенням функції, тобто =(0;%20\%20+\infty).)
Це означає, що графік показникової функції 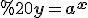 завжди розташований вище осі Ох і будь-яка пряма, що паралельна осі Ох і знаходиться вище неї, перетинає цей графік.
завжди розташований вище осі Ох і будь-яка пряма, що паралельна осі Ох і знаходиться вище неї, перетинає цей графік.
Обґрунтування області значень та проміжків зростання і спадання показникової функції проводиться в курсі вищої математики так: ці властивості перевіряються послідовно для натуральних, цілих, раціональних показників, а потім уже переносяться на довільні дійсні показники.
Точки перетину з осями координат. Графік функції 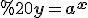 перетинає вісь
перетинає вісь 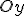 у точці
у точці 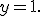 Дійсно, на осі
Дійсно, на осі 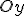 значення
значення 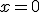 , тоді
, тоді 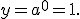
Графік показникової функції ) не перетинає вісь
не перетинає вісь 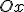 , оскільки усі точки осі
, оскільки усі точки осі 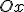 мають ординату 0, але значення
мають ординату 0, але значення 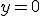 не входить до області значень показникової функції
не входить до області значень показникової функції 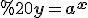 (
( 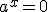 тільки при
тільки при 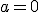 , але за означенням
, але за означенням 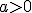 ).
).
Функція 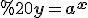 не має ні найбільшого, ні найменшого значень, оскільки її область значень - проміжок
не має ні найбільшого, ні найменшого значень, оскільки її область значень - проміжок ,) який не містить ні найменшого, ні найбільшого числа.
який не містить ні найменшого, ні найбільшого числа.
Властивості показникової функції
Слід зазначити, що для функції ) справедливою є рівність
справедливою є рівність %20\cdot%20f(x_2)=f(x_1+x_2),) при довільних дійсних значеннях аргумента
при довільних дійсних значеннях аргумента 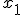 та
та 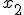 . Строге доведення цих рівностей здійснюється в курсі вищої математики.
. Строге доведення цих рівностей здійснюється в курсі вищої математики.
Розглянемо наступні графіки функцій:
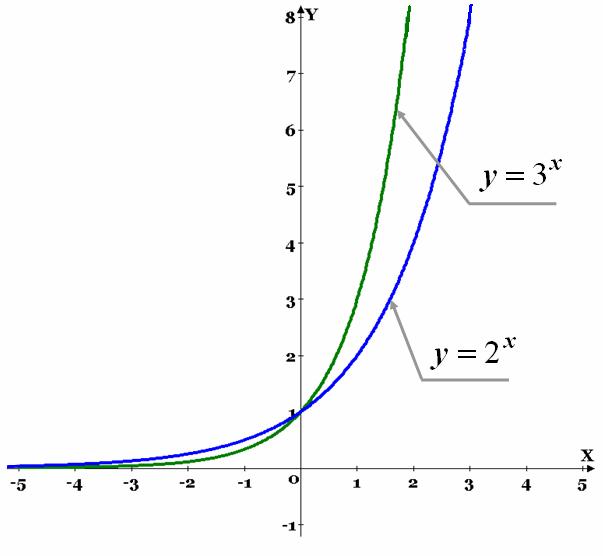
Порівнюючи ці графіки, робимо висновок: чим більша основа 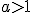 , тим крутіше піднімається графік функції при русі точки зліво направо і тим швидше графік наближається до осі Ох при русі точки справа наліво.
, тим крутіше піднімається графік функції при русі точки зліво направо і тим швидше графік наближається до осі Ох при русі точки справа наліво.
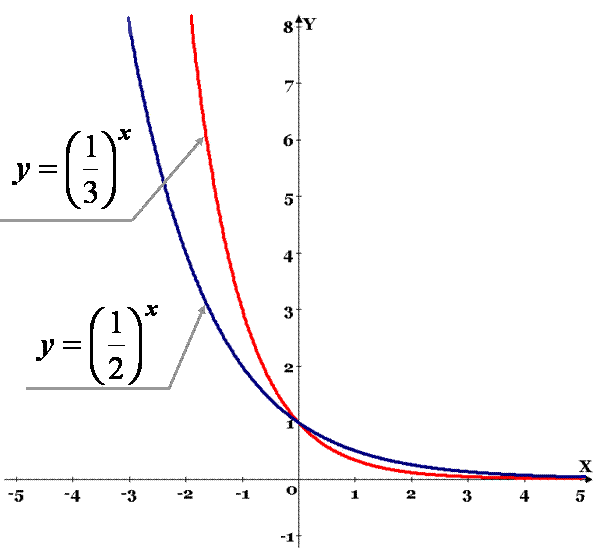
Аналогічно, чим менша основа 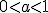 , тим крутіше піднімається графік функції при русі точки справа наліво і тим швидше графік наближається до осі Ох при русі точки зліва направо.
, тим крутіше піднімається графік функції при русі точки справа наліво і тим швидше графік наближається до осі Ох при русі точки зліва направо.
Зауважимо, що вираз 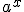 можна розглядати і при
можна розглядати і при 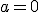 і при
і при 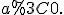 Але в цих випадках він уже буде означений не при всіх дійсних значеннях
Але в цих випадках він уже буде означений не при всіх дійсних значеннях 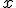 , як показникова функція
, як показникова функція 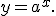 Зокрема, вираз
Зокрема, вираз 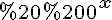 означений при всіх
означений при всіх 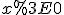 (і тоді
(і тоді 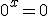 ), а вираз
), а вираз ^x) - при всіх цілих значеннях
- при всіх цілих значеннях 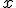 ( наприклад,
( наприклад, ^{-3}=\frac{1}{(-2)^3}=-\frac{1}{8}) ). З цієї причини й не беруть основу показникової функції
). З цієї причини й не беруть основу показникової функції 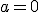 (одержуємо постійну функцію при
(одержуємо постійну функцію при 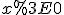 ) та
) та 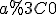 (одержуємо функцію, означену тільки при досить «рідких» значеннях
(одержуємо функцію, означену тільки при досить «рідких» значеннях 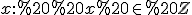 . Але наведені міркування стосовно доцільності вибору основи показникової функції не впливають на область допустимих значень виразу
. Але наведені міркування стосовно доцільності вибору основи показникової функції не впливають на область допустимих значень виразу 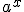 (наприклад, як ми бачили вище, пара значень
(наприклад, як ми бачили вище, пара значень 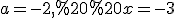 входить до його ОДЗ, і це доводиться враховувати при розв'язуванні деяких завдань).
входить до його ОДЗ, і це доводиться враховувати при розв'язуванні деяких завдань).
Приклади розв'язання завдань
Пр1. Порівняйте значення виразів:
а) ^{-3}) та
та ^{-5}.)
Функція ^x) є спадною (основа степеня менша за 1), тому з нерівності
є спадною (основа степеня менша за 1), тому з нерівності 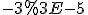 одержуємо
одержуємо ^{-3}%3C%20\left%20(\frac{2}{3}%20\right%20)^{-5}.)
б) ^4) та
та ^3) .
.
Функція ^x) є зростаючою
є зростаючою ,) тому з нерівності
тому з нерівності 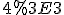 одержуємо
одержуємо ^{4}%3E%20\left%20(\frac{\sqrt{7}}{2}%20\right%20)^{3}.)
Слід врахувати, що функція 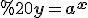 при а > 1 є зростаючою, а при 0 < а < 1 - спадною. Отже, спочатку порівняємо задану основу а з одиницею, а потім, порівнюючи аргументи, зробимо висновок про співвідношення між заданими значеннями функції.
при а > 1 є зростаючою, а при 0 < а < 1 - спадною. Отже, спочатку порівняємо задану основу а з одиницею, а потім, порівнюючи аргументи, зробимо висновок про співвідношення між заданими значеннями функції.
Пр 2. Порівняйте з одиницею додатну основу  , якщо відомо, що виконується нерівність:
, якщо відомо, що виконується нерівність:
а) 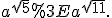
Оскільки 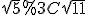 і за умовою
і за умовою 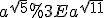 , то функція
, то функція 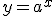 є спадною, отже,
є спадною, отже, 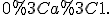
б) 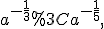
Оскільки 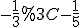 і за умовою
і за умовою 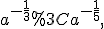 то функція
то функція 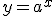 є зростаючою, отже,
є зростаючою, отже, 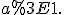
Немає коментарів:
Дописати коментар