Рівняння af(x) = ag(x), де а > 0, а ≠ 1.
Рівняння af(x) = ag(x), де а > 0, а ≠ 1, рівносильне рівнянню f(х) = g(x).
Приклад. Розв’яжіть рівняння:
Розв’язання. 
Способи розв'язування показникових рівнянь
Одним з основних методів розв'язування показникових рівнянь полягає в тому, що рівняння за допомогою рівносильних перетворень намагаються звести до виду
Останнє рівняння рівносильне рівнянню:
Приклад 1. Розв'язати рівняння:
Відповідь. -1.
Приклад 2. Розв'язати рівняння: 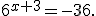
Дане рівняння коренів немає, оскільки ліва частина 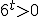 для всіх
для всіх 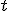 , а права -36<0.
, а права -36<0.
Відповідь. коренів немає.
Якщо в лівій і правій частинах показникового рівняння стоять тільки добутки, частки, корені або степені, то доцільно за допомогою основних формул спробувати записати обидві частини рівняння як степені з однією основою.
Приклад 3. Розв'язати рівняння:
Відповідь. 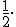
Якщо в одній частині показникового рівняння стоїть число, а в іншій всі члени містять вираз виду 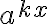 (показники степенів відрізняються тільки вільними членами), то зручно в цій частині рівняння винести за дужки найменший степінь а.
(показники степенів відрізняються тільки вільними членами), то зручно в цій частині рівняння винести за дужки найменший степінь а.
Приклад 4. Розв'язати рівняння:
Відповідь. 2.
Показниковими зазвичай називають рівняння, у яких змінна входить у показник степеня (а основа цього степеня не містять змінної).
Розглянемо найпростіше показникове рівняння
де 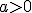 і
і 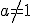 . Оскільки при цих значеннях
. Оскільки при цих значеннях  функція
функція 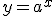 строго монотонна (зростає при
строго монотонна (зростає при 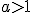 і спадає при
і спадає при 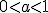 ), то кожного свого значення вона набуває тільки при одному значенні аргументу. Це означає, щорівняння
), то кожного свого значення вона набуває тільки при одному значенні аргументу. Це означає, щорівняння 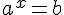 при b>0 має єдиний корінь. Щоб його знайти, досить подати b у вигляді
при b>0 має єдиний корінь. Щоб його знайти, досить подати b у вигляді 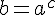 .
.
Очевидно, що 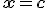 є коренем рівняння
є коренем рівняння 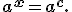
Наприклад, щоб розв'язати рівняння 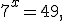 досить подати це рівняння у вигляді
досить подати це рівняння у вигляді 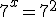 і записати його єдиний корінь
і записати його єдиний корінь 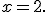
Якщо 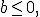 то рівняння
то рівняння 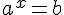 (при a> 0) коренів не має, оскільки
(при a> 0) коренів не має, оскільки 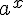 завжди більше нуля. (На графікупряма
завжди більше нуля. (На графікупряма 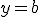 не перетинає графік функції
не перетинає графік функції 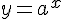 при
при 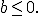 )
)
Наприклад, рівняння 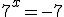 не має коренів.
не має коренів.
Узальнюючи наведені вище міркування стосовно розв'язування найпростіших показникових рівнянь, відзначимо, що при 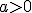 і
і 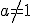 рівняння
рівняння
рівносильне рівнянню
Щоб обґрунтувати цю рівносильність, досить помітити, що рівності (2) і (3) можуть бути правильними тільки одночасно, оскільки функція 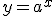 є строго монотонною і кожного свого значення вона набуває тільки при одному значенні аргументу
є строго монотонною і кожного свого значення вона набуває тільки при одному значенні аргументу 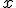 (тобто з рівності степенів (2) обов'язково випливає рівність показників (3)).
(тобто з рівності степенів (2) обов'язково випливає рівність показників (3)).
Отже, усі корені рівняння (2) (які перетворюють це рівняння на правильну рівність) будуть і коренями рівняння (3), та навпаки, усі корені рівняння (3) будуть коренями рівняння (2).
А це й означає, що рівняння (2) і (3) рівносильні.
Отже, у найпростіших випадках при розв'язуванні показникових рівнянь намагаються за допомогою основних формул дій над степенями звести (якщо це можливо) задане рівняння до виду }=a^{g(x)}) .
.
Для розв'язування більш складних показникових рівнянь найчастіше використовують заміну змінної або властивості відповідних функцій.
Зауважимо, що всі рівносильні перетворення рівняння завжди виконуються на його області допустимих значень (тобто на спільній області визначення для всіх функцій, які входять до запису цього рівняння). Але в показникових рівняннях найчастіше областю допустимих значень (ОДЗ) є множина всіх дійсних чисел. У цих випадках, як правило, ОДЗ явно не знаходять і не записують до розв'язання рівняння (див. нижче приклади). Але якщо в процесі розв'язування показникових рівнянь рівносильні перетворення виконуються не на всій множині дійсних чисел, то в цьому випадку доводиться згадувати про ОДЗ .
Приклади розв'язання рівнянь
Приклад 5. Розв'язати рівняння:
Відповідь. 5.
У лівій і правій частинах рівняння стоять тільки добутки, частки, корені або степені. У цьому випадку для зведення рівняння до виду }=a^{g(x)}) спробуємо використати основні формули дій над степенями, щоб записати обидві частини рівняння як степені з однією основою. Слід звернути увагу на те, що
спробуємо використати основні формули дій над степенями, щоб записати обидві частини рівняння як степені з однією основою. Слід звернути увагу на те, що
та 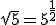 , отже, ліву і праву частини цього рівняння можна записати як степені числа 5.
, отже, ліву і праву частини цього рівняння можна записати як степені числа 5.
Приклад 6. Розв'язати рівняння:
Для перетворення рівняння згадаємо, що всі формули можна використовувати як зліва направо, так і справа наліво, наприклад, для лівої частини цього рівняння скористаємося тим, що ^x=6^x.)
Відповідь. 1.
Приклад 7. Розв'язати рівняння:
Задане рівняння рівносильне рівнянням:
Відповідь. 1.
У лівій частині рівняння всі члени містять вирази виду 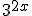 (показники степенів відрізняються тільки вільними членами). У цьому випадку зручно винести за дужки в лівій частині рівняння найменший степінь числа 3, тобто
(показники степенів відрізняються тільки вільними членами). У цьому випадку зручно винести за дужки в лівій частині рівняння найменший степінь числа 3, тобто 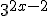 .
.
Приклад 8. Розв'язати рівняння з параметром:
ОДЗ: 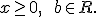
1) При 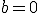 отримуємо рівняння
отримуємо рівняння 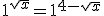 , корені якого - усі дійсні числа з ОДЗ, тобто
, корені якого - усі дійсні числа з ОДЗ, тобто 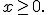
2) При 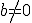 значення
значення 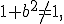 і тоді задане рівняння рівносильне рівнянню
і тоді задане рівняння рівносильне рівнянню 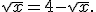
Звідси 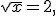 тоді
тоді 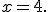
Відповідь. 1) при 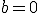 ,
, ;)
2) при 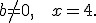
Це рівняння відносно змінної 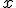 , яке містить параметр
, яке містить параметр 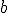 . Аналізуючи основу степенів у цьому рівнянні, робимо висновок, що при будь-яких значеннях
. Аналізуючи основу степенів у цьому рівнянні, робимо висновок, що при будь-яких значеннях 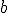 основа
основа 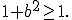 Функція
Функція 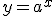 при
при 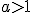 є зростаючою, а при
є зростаючою, а при 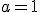 - постійною.
- постійною.
Основа 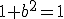 при
при 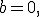 а
а 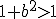 при
при 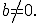
Розглядали кожен із цих випадків окремо, тобто: 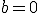 і
і 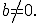
БАНК ПОКАЗНИКОВИХ РІВНЯНЬ
Розв’язати
показникові рівняння
Рівень А
1. а)2-х +3 = 2x - 3; б) 4-4х +5 =4 4x - 3; в) 5-х +5 = 5 x – 5.
2. 8х = 4x-8 ; б) 16 x = 324 -5x ; в) 27 х +7 = 81x – 7.
3. 49x = 343x; б) 729x = 27x; в) 256x = 64x.
4. 3х∙2x = 6x +1; б)4х∙2x = 8x -8; в)5х∙2x = 10x +7.
5. 60 = 4- x + 2; б)10 = 5- 5x + 5; в) 70 = 3- 7x + 2;
6. 3х∙22x = 12x - 5; б) 9х∙22x = 18x - 5; в) 4х∙22x = 16x - 5;
7. - 4 = 4- x + 3; б) - 5 = - 2- x + 2; в) - 3 = - 2- x + 4;
8. 1210 = 11x - 1; б) 25x - 3∙125 = 625 - x +1; в) 10 = 2∙(0,2)3x + 2;
9. 75 x = 3x - 2∙52x - 4; б) 72 x = 8x - 2∙32x - 4; в) 60 x = 15x - 2∙22x - 4;
10.
3- x = -5- x ; б) 1- x = - 6- x ; в) 7- x = -2- x ;
11.
164х =
4-3 + х ∙43x + 2;
б) 25∙5x - 5 = 125∙5x - 5; в) 4∙512x = 16∙256-
x +1;
12. 16х + 14∙4х – 32 = 0; б) 4х
+ 2х – 8 = 0; В) 7. 9х + 8∙3х + 1 – 81 = 0;
Рівень Б
1. 5∙(2)x-3 - 0,5∙2x = (4x)x ∙4-2; 2. (3x-3)x+4 = 3-x ∙ 9x-4;
3. 4-x ∙(4x)x = 8∙(0,5)3x; 4. (0,5)х×х×22х + 2 = 64 -1;
5. 5х×2х =
0,1×(1 х -1)5
; 6. 4х + 2х
– 8 = 0.
7. 9х + 8∙3х + 1 – 81 = 0; 8. 16х + 14∙4х – 32 = 0;
9. 25х + 5,2∙5х + 1 = 0. 10. 4х - 2х + 2 - 32 = 0.
Рівень В
1.(х2 - 6x + 8)х – 2 = 1;
2. (x-2)х×х - 6x + 8 = 1;
Немає коментарів:
Дописати коментар