
Розглянемо графік рівняння одиничного кола х2 + у2 =
1, з центром в точці (0; 0) і радіусом R=1 в прямокутній системі координат
ХОУ.
Уявимо, що по цьому колу обертається точка М(х; у). Визначимо точку, яка буде називатися початком
обертання.
Означення. Точку перетину одиничного кола х2 + у2 = 1 з додатним напрямом осі Ох (абсцис) А(1; 0) вважатимемо початком
руху точки М(х; у) по одиничному колу.
Визначимо додатний і від’ємний напрям обертання. Уявіть, що ми провели
числову пряму , як дотичну до кола в А(1; 0). Тепер вважатимемо, що числова
пряма є ниткою і накручуємо цю нитку на одиничне
коло х2 + у2 = 1.
Від точки А(1; 0) проти часової стрілки накручується
додатна частина числової прямої. Цей напрям називають додатним напрямом руху
точки М(х; у) по одиничному колу.
Від точки А(1; 0) за часовою стрілкою накручується
від’ємна частина числової прямої. Цей напрям називають від’ємним напрямом руху
точки М(х; у) по одиничному колу.
Місце положення точки
М(х; у) на одиничному колі можна виразити не тільки абсцисою х та
ординатою у. Вкажемо, ще один спосіб
знаходження місце положення точки М на
одиничному колі. Наприклад, уявімо, що на числовій прямій, що
намотується на одиничне коло, позначили не числову, а градусну міру, як в
додатному так і у від’ємному напрямі,
Зрозуміло, що нульовий градус потрапляє у число нуль на числовій прямій, прямий
кут, тобто 90о, в додатному напрямі є число 0,5p,
прямий кут за від’ємним напрямом є число -0,5p, розгорнутий кут в додатному напрямі є число p,
розгорнутий кут за від’ємним напрямом є число -p, і так далі. Так ми встановили взаємно
однозначну відповідність між градусною мірою повороту радіуса одиничного
кола відносно початку координат О(0; 0)
з числовою мірою(її часто називають
радіанною мірою кутів) на числовій прямій.
Отож, кожне положення точки М(х;
у) під час руху по одиничному колу, може задаватися однією координатою та
напрямом руху, а саме градусною мірою повороту радіуса одиничного кола, що
відповідає точці на градусній прямій, яку намотали на це коло.
Якщо точка М(х; у) рухається по колу від точки початку А(1; 0) в
напрямі проти часової стрілки до деякої точки Ра , то цей напрям
руху задається як певна величина дуги АМ(частина кола), яку
вкаже додатне значення на накрученій градусній прямій.
Якщо точка М(х; у) рухається по одиничному колу від
точки початку А(1; 0) в напрямі за часовою стрілкою до деякої точки Р-в , то цей напрям руху задається як певна
міра, величина дуги АМ(частина кола), яку вкаже від’ємне значення на накрученій градусній прямій.
Встановимо зв’язок між абсцисою х та ординатою у точки М(х; у) і градусною мірою( а отже і радіанною
мірою) дуги АМ на одиничному колі.
Положення точки визначається однозначно, якщо вказати довжину дуги АМ,
нехай вона дорівнює х( дивись малюнок),
якщо відраховувати в додатному напрямі від початкової точки А до точки М. Коли
значення х зростає від 0 до 2p, то точка М робить повний оберт по колу в
додатному напрямі.
Проміжку 0 <
х < 0,5p відповідає дуга АВ, і тоді говорять, що точка
М вона знаходиться в першій чверті.
Проміжку 0,5p < х < p відповідає дуга ВС, і тоді говорять, що точка М вона
знаходиться в другій чверті.
Проміжку p < х < 1,5 p відповідає дуга CD, і тоді говорять, що точка М вона знаходиться в
третій чверті.
Проміжку 1,5p < х < 2 p відповідає дуга DА, і тоді говорять, що точка М вона знаходиться в
четвертій чверті.
Із точки М, що знаходиться в першій чверті, опустимо перпендикуляр на
вісь Ох, отримаємо основу перпендикуляра М1.
Розглянемо прямокутний трикутник ОММ1, гіпотенуза ОМ = 1, кут
ОМ1М – прямий. Позначимо за а
кут М1ОМ. Називатимемо катет М1О – прилеглий катет до
кута а. Називатимемо катет М1М
– протилежний катет до кута а.
Означення. Косинусом
гострого кута а прямокутного трикутника
називається відношення довжин прилеглого катета та гіпотенузи і позначається
cos а = М1О:ОМ = х
: 1 = х, де х – абсциса точки М(х;
у).
Означення. Синусом гострого кута прямокутного трикутника
називається відношення довжин протилежного катета та гіпотенузи і позначається
sin а = М1М:ОМ = у : 1 = у, де у – ордината точки М(х; у).
Означення. Тангенсом
гострого кута прямокутного трикутника називається відношення довжин протилежного
та прилеглого катетів:
tg а = М1М:ОМ1 , tg а = (sin а) : (cos
а) .
Означення. Котангенсом
гострого кута прямокутного трикутника називається відношення довжин прилеглого
та протилежного катетів:
ctg а = М1О:ММ1, ctg а
= (cos а) : (sin а),
ctg а = 1 : tg а.
Означення. Секансом
гострого кута а прямокутного трикутника
називається відношення довжин гіпотенузи та
прилеглого катета і позначається
sес а = ОМ :М1О. sес
а = 1 : cos а.
Означення. Косекансом
гострого кута а прямокутного трикутника
називається відношення довжин гіпотенузи та
протилежного катета і позначається
cosес а = ОМ :М1М.
соsес а = 1 : sin а.
Знаки тригонометричних виразів
Звертаємо увагу, що в означеннях фігурують гострі кути прямокутного
трикутника. Для того щоб розширити ці означення на довільні значення кутів
повороту радіуса навколо початку, можна побудувати такі ж прямокутні трикутники
в другій, третій, четвертій чвертях і отримати відповідні значення абсциси та ординати точки М(соs a; sin a).
Абсциса Х і ордината У точки М, що розташована на одиничному колі таким
чином є функціями від градусу повороту радіуса одиничного кола, і їх називають
косинусом та синусом .
А тепер згадаємо, що графік рівняння одиничного кола х2 + у2 = 1. Враховуючи, що точка М(х; у) = М(соs a; sin a) рухалася на цьому колі, тоді виконаємо в цьому
рівнянні заміну змінних:
х2
+ у2 = соs2 a + sin2 a =
1.
Означення. Рівність соs2 a + sin2 a
= 1 називається основною
тригонометричною тотожністю.
Означення. Рівність tg a∙ctga = 1 називається основною тригонометричною тотожністю.
Таким чином, означення основних тригонометричних функцій має
геометричний зміст, адже пов’язане з колом, тому тригонометричні функції іноді
називають круговими функціями. Однак існує інші, формульні означення синуса та
косинуса, наприклад, найпростіші із формул можуть бути взяті степеневі ряди, в
яких розуміють виконання тільки двох операцій – додавання і віднімання, проте
кількість цих дій безмежна, що рівносильно
існуванню граничному переходу до певної межі.
Тангенси
та котангенси гострих кутів ( < 90 0 ) та їх
основні властивості

4. Тангенси та котангенси додаткових кутів
5. В практичних обчисленнях часто використовують значення тангенсів та котангенсів, що наведені в таблиці

Означення. Функцією тангенса називається
функція, що задається формулою у = tg x.
Відомо, що число p -
трансцендентне, тобто воно не може бути розв’язку деякого раціонального рівняння
з раціональними коефіцієнтами. Звертаєтамо
увагу на те, що функція у = tg x може приймати значення аргументу
із множини трансцендентних чисел.
Функція тангенса належить до множини трансцендентних функцій.
Функція тангенса
належить до множини тригонометричних функцій.
В прямокутній системі
координат графіком функції у = tg x являється множина точок Г = {(x; tg x.)| xєR}.
Означення. Пряма х =1 називається вісь
тангенсів, якщо вона дотична до одиничного кола.
Будь-яка точка А
на вісі тангенсів, має координати
А(1; tg x),
де х – міра кута нахилу прямої ОА з додатним напрямом
вісі Ох.
Означення. Тангенсоїдою називається множина точок
Г = {(x; tg x.)| xєR}.

ВЛАСТИВОСТІ ФУНКЦІЇ у = tg x.
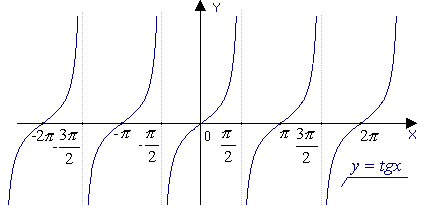
Область визначення функції тангенса – не є множина всіх
дійсних чисел.
tg х
= (sin х) : (cos х) , де
cos х ≠ 0, тобто, х ≠ 0,5p + pk, де kєZ.
Отже, графік цієї
функції невизначений в точках х = 0,5p + pk,, тобто не існує. А безліч прямих х = 0,5p + pk, де kєZ являються вертикальними
асимптотами, тобто лініями до яких функція наближається як завгодно близько,
але їх не перетинає.
Позначення області
визначення функції тангенса:
D(tg x) = R / {0,5p + pk } =
(-0,5p + pk; 0,5p + pk ), де kєZ.
Множина значень функції тангенса – це множина усіх дійсних чисел, що належать числовій прямій R.
Позначення області значення
функції тангенса: Е(tg x) = R.
Функція у = tg x непарна.

Графік функції у = tg x симетричний відносно точки (0; 0), тобто
початку координат.
Функція у = tg x періодична з найменшим додатним періодом Т = p.
Форма графіка
повторюється через p. Сам графік можна одержати з будь-якої частини графіка
на інтервалі завдовжки p за допомогою паралельного перенесення вздовж
осі абсцис вліво або вправо на 2pk, де kєZ.
Точки перетину з осями координат.
Графік функції у = tg x перетинає вісь абсцис, якщо у = 0, тоді
tg x = 0;
х = pk, де kєZ.
Отже, нулі функції у = tg x:
Функція у = tg x має безліч нулів, тобто, точок
перетину тангенсоїди з віссю абсцис(Ох) безліч.
Точки перетину графіка
функції у = tg x з віссю Ох:
(pk; 0), де
kєZ.
Графік функції у = tg x перетинає вісь ординат, якщо х
= 0, тоді
у = tg 0 = 0;
Точка перетину графіка
функції у = tg x з віссю Оу: (0; 0).
Проміжки знакосталості.
Функція у = tg x додатна, якщо
cos x
> 0, х Î (pk; 0,5p + pk), де kєZ.
Функція у = tg x від’ємна, якщо
cos x
< 0, х Î (-0,5p + pk; pk), де kєZ.
Функція у = tg x неперевна в кожному з проміжків:
(-0,5p + pk; 0,5p + pk), де kєZ.
і необмежена зверху і необмежена знизу/

Поведінка функції у = tg x біля початку координат
Якщо x ® 0,
то tg x ® 0.
Якщо x ® +0,
то (tgx)/x ® 1.
Якщо x ® -0,
то (tgx)/x ® 1.
У
графіка функції у = tg x безліч точок розриву
х = 0,5p + pk, де kєZ.
другого роду.
У
графіка функції у = tg x є вертикальні асимптоти:
При х ® -0,5p(наближається справа) , то tg x® -oo.
При х ® -0,5p(наближається зліва) , то tg x® oo.
У
графіка функції у = tg x є безліч вертикальних
асимптот:
х = 0,5p + pk, де kєZ.
Функція у = tg x має
похідну для будь-якого значення із
R / {0,5p + pk }, де kєZ
.
Проміжки монотонності функції у = tg x.
Функція у = tg x зростає в кожному з проміжків:
(-0,5p + pk; 0,5p + pk), де kєZ.
Функція у = tg x не спадає на жодному проміжку.
Екстремуми функції
немає.
Функція у = tg x не має найбільшого
значення.
Функція у = tg x не має найменшого
значення.

1. Як називається функція, що задана формулою у
= tgx?
2. а) Як називається графік функції у
= tgx? б) Що таке вісь тангенсів?
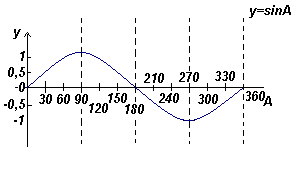
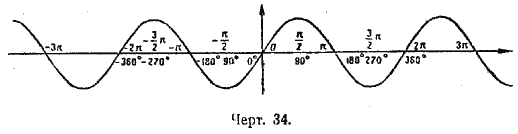
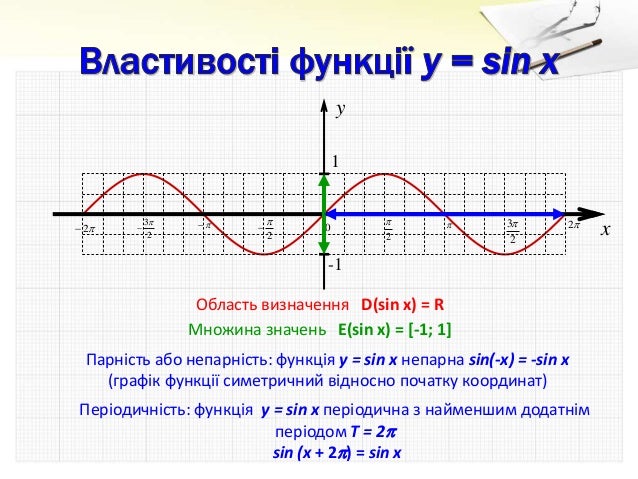
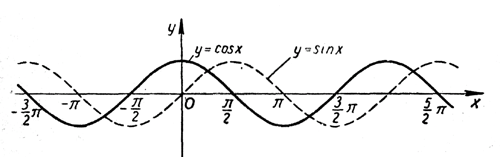
3. Яка різниця між
графіками функції у = tg x та функції у = sin x?
4. Якою симетрією володіє графік функції у
= tgx?
5. Які нулі функції у
= tgx? Скільки нулів у тангенсоїди?
6. Чи вірно, що
функція у = tgx
належить множині раціональних функцій?
7. Чи вірно, що множина раціональних чисел входить до
області визначення функції у = tgx?
8. Чи вірно, що множина цілих чисел входить до множини
значення функції у = tgx?
9. Чи вірно, що
функція у = tgx
обмежена знизу?
10. Чи вірно, що
функція у = tgx
розривна на області визначення?
11. Чи вірно, що
функція у = tgx
має тільки один період на всій
області визначення?
12. Як побудувати графік функція у = tgx?
13. Що означає термін
«функція у = tgx має проміжки знакосталості»?
14. Що означає термін
«функція у = tgx має проміжки, на яких вона невід’ємна»?
15. Що означає термін
«функція у = tgx має проміжки, на яких вона недодатна»?
16. Що означає термін
« графік функції у = tgx
має безліч асимптот»?
17. Що означає термін
«функція у = tgx
має проміжки неспадання»?
18. Що означає термін
«функція у = tgx
має проміжки монотонності»?
19. Чи вірно, що функція
у = tg4x може дорівнювати 4p?
20. Чи вірно, що функція
у = 6 tgx має період 6p?
21. Чи вірно, що функція
у = tgx
має найбільше значення?
22. Чи вірно, що функція
у = tgx
не має найменше значення?
23. Чому дорівнює
значення функції у = tgx, якщо x ® 0?
24.Чи вірно, що tg x
< -10?
25. Чи вірно, що tg x
> 100?
26. Чи завжди вірно,
що tg (-x) = tg x?
27. Чи вірно, що tg (x+ p) = tg (x+ pk) = cos x, де k
ÎZ?
28. Чи вірно, що функція у = tg x зростає
в кожному з проміжків
[-0,5p + pk; pk], де k ÎZ?
29. Чи
вірно, що функція у = tg x спадає
в кожному з проміжків
[pk; p + pk], де k ÎZ.
30. Чи вірно, що екстремуми функції у = tg x це деякі цілі числа?
31. Чи вірно, що функція
у = tg x набуває найбільшого значення, що дорівнює ymax = 50 в точках хmax = 0,5p +pk, де k ÎZ?
32. Чи вірно, що функція
у = tg x набуває найменшого значення, що дорівнює ymin = -50 в точках хmin = -0,5p + pk, де k ÎZ?









 Перша похідна функції
Перша похідна функції 

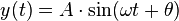



Немає коментарів:
Дописати коментар