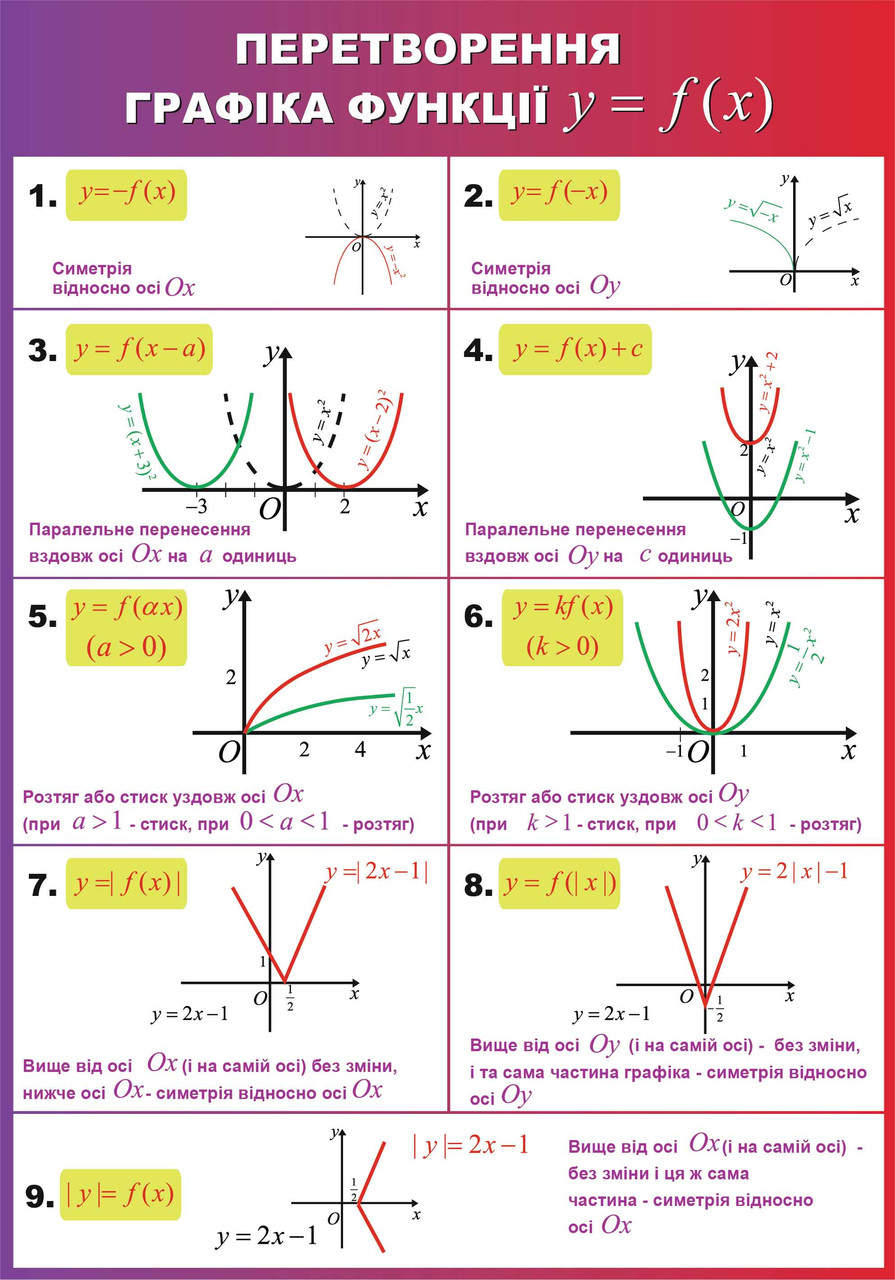
Графік функції з абсолютною величиною

Графік функції з абсолютною величиною

Властивості модулів










Алгоритм побудови графіків з модулями

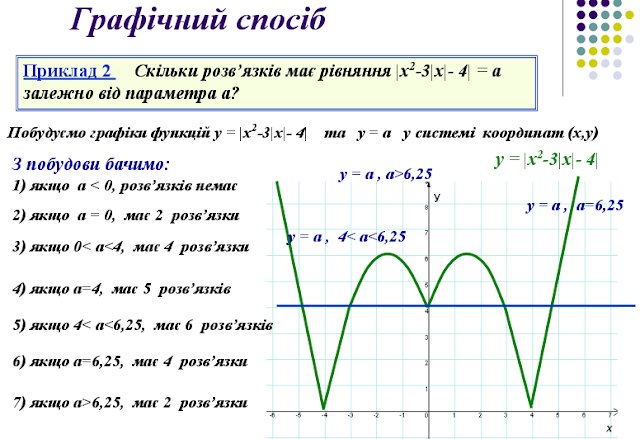
Рівняння  виду  

 a|py-n| + b|kx-m|= c

Дослідити розв’язки рівняння 

a|py-n| + b|kx-m|= c

відносно двох дійсних невідомих х та у,  
якщо відомі дійсні параметри: a, b, c, k, m, n, p.

Якими геометричними  фігурами зображається  графік рівняння:  a|py-n| + b|kx-m|= c, що побудований   в прямокутній системі координат хОу?(Чи може бути така множина фігур: ромб, одна точка, дві прямі, що перетинаються,  два центрально-симетричні кути, порожня множина точок, уся площина).

Якщо використати заміну змінних:  q=py-n   w= kx-m, тоді отримаємо рівняння

a|q| + b|w|= c з двома дійсними невідомими (q; w) .

Узагальнення видів  графіків  рівняння  a|py-n| +b|kx-m|= c, якщо не нульові парметри k та p
С<0	a>0	a<0	a=0		С=0	a>0	a<0	a=0
b>0	порожня множина	два кути	дві прямі		b>0	одна точка	дві прямі	одна пряма
b<0	два кути	ромб	дві прямі		b<0	дві прямі	одна точка	одна пряма
b=0	дві прямі	дві прямі	порожня множина		b=0	одна пряма	одна пряма	уся площина
С>0	a>0	a<0	a=0
b>0	ромб	два кути	дві прямі
b<0	два кути	порожня множина	дві прямі
b=0	дві прямі	дві прямі	порожня множина

Випадок порожньої множини точок. Дане рівняння немає дійсні  розв’язки, якщо виконуються умови: 1) а<=0, b<=0, c>0 або виконуються умови: 2) 1) а>=0, b>=0, c<0. Це слідує з того факту, що ліва та права частини рівняння мають різні знаки на усій дійсній множині пар (х; у) . У цьому випадку графіку у даного рівняння не існує(порожня множина точок площини), бо не існує пари чисел, які задовольняють рівняння.

Випадок рівняння ромба: За одночасного виконання умов: {а>0; b>0;  с>0, c/bk >0, c/pa > 0} або {а<0; b<0;  с<0, c/bk >0, c/pa > 0}   дане рівняння задовольняють безліч пар дійсних чисел, які позначатимемо: (x₁;y₁) (x₂;y₂), (x₃;y₃), (x₄;y₄),  відповідно до  чотирьох умов:

(x₁;y₁) = (x₁; (-bkx₁+c+bm+an)/ap),  якщо   {(x₁;y₁) | n/p<=y₁<+oo;  m/k<=x1<+oo}

(x₂;y₂) = (x₂; (bkx₂+c-bm+an)/ap),  якщо    {(x₂;y₂) | n/p<=y₂<+oo;   -oo<x₂<m/k}

(x₃;y₃) = (x₃; (-bkx₃+c+bm-an)/(-ap)),  якщо  {(x₃;y₃) | -oo<y₃< n/p;   m/k<=x₃<+oo}

(x₄;y₄) = ( x₄; (bkx₄+c-bm-an)/(-ap)),  якщо   {(x₄;y₄) |  -oo<y₄< n/p;   -oo<x₄<m/k}

Тоді графік такого рівняння описує фігура ромб:

·         з центром в точці, що має координати: (m/k; n/p)

·          довжиною горизонтальної півдіагоналлі  c/bk >0

·         довжиною  вертикальної півдіагоналлі  c/pa > 0

Випадок рівняння двох центральносиметричних кутів: за одночасного виконання умов:  { аb<0; c<>0; c/bk >0, c/pa<0}   або { аb<0; c<>0; c/bk<0, c/pa>0}  дане рівняння задовольняють безліч пар дійсних чисел, які позначатимемо: (x₁;y₁) (x₂;y₂), (x₃;y₃), (x₄;y₄),  відповідно до  чотирьох умов:

(x₁;y₁) = (x₁; (-bkx₁+c+bm+an)/ap),  якщо   {(x₁;y₁) | n/p<=y₁<+oo;  m/k<=x1<+oo}

(x₂;y₂) = (x₂; (bkx₂+c-bm+an)/ap),  якщо    {(x₂;y₂) | n/p<=y₂<+oo;   -oo<x₂<m/k}

(x₃;y₃) = (x₃; (-bkx₃+c+bm-an)/(-ap)),  якщо  {(x₃;y₃) | -oo<y₃< n/p;   m/k<=x₃<+oo}

(x₄;y₄) = ( x₄; (bkx₄+c-bm-an)/(-ap)),  якщо   {(x₄;y₄) |  -oo<y₄< n/p;   -oo<x₄<m/k}

Тоді графік такого рівняння описує фігура, що утворює два кути, які симетричні відносно центру симетрії, що має координати: (m/k; n/p).

 Якщо c/bk <=0 і c/pa >=0,  тоді один кут внутрішньою областю  дивиться вгору, а інший кут дивиться вниз і  вершини двох кутів розташовуються в відповідних  точках: (m/k; c/pa+n/p), (m/k; -c/pa+n/p),        

Якщо c/pa <=0 і c/bk >=0, один кут дивиться внутрішньою областю ліворуч, а інший кут дивиться впаворуч, і  вершини двох кутів розташовуються в відповідних точках: (c/bk+m/k; n/p), (-c/bk+m/k; n/p).        

Випадок рівняння однієї точки. Якщо {a>0; b>0; с=0}  або {a<0; b<0; с=0} ,  то графік рівняння є однією точкою, яка має координати: (m/k; n/p). Розв’язком рівняння являється пара чисел: (m/k; n/p).

Випадок рівняння двох прямих, що перетинаються. Якщо {a<0; b>0; с=0}  або {a>0; b<0; с=0} ,  то графік рівняння є дві прямі, які перетинаються в точці: (m/k; n/p).

Випадок рівняння площини. Якщо {a=0; b=0; с=0} ,  то графік рівняння є усі точки прямокутної системи координат.