Графік функції з абсолютною величиною
Властивості модулів

Алгоритм побудови графіків з модулями

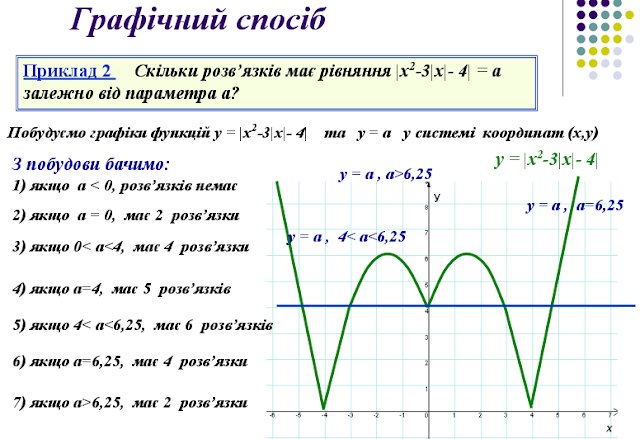
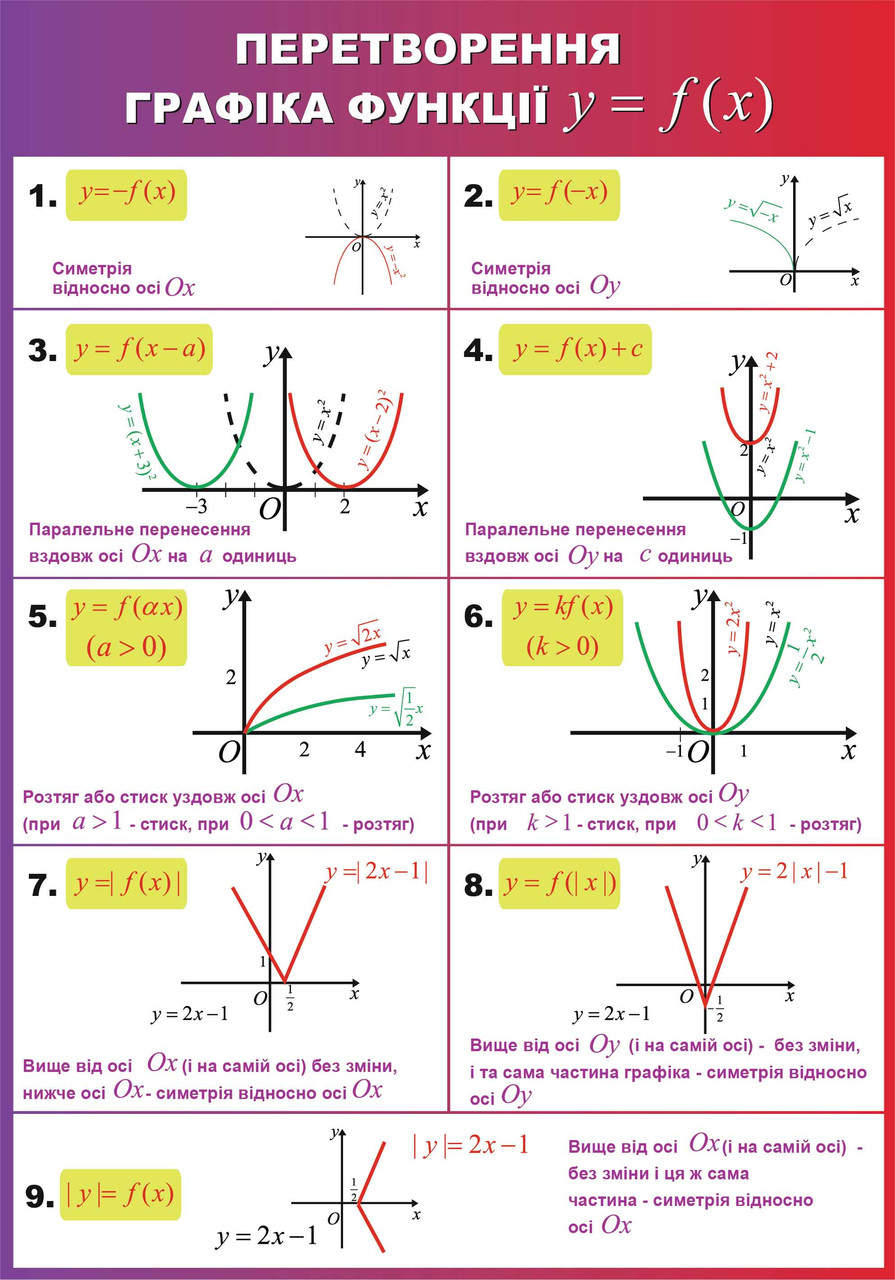


Рівняння
виду
a|py-n| + b|kx-m|= c
Дослідити розв’язки
рівняння
a|py-n| + b|kx-m|= c
відносно двох дійсних
невідомих х
та у,
якщо відомі дійсні параметри: a, b, c, k, m, n, p.
якщо відомі дійсні параметри: a, b, c, k, m, n, p.
Якими
геометричними фігурами зображається графік рівняння:
a|py-n| + b|kx-m|= c, що побудований в прямокутній
системі координат хОу?(Чи може бути така множина фігур: ромб, одна точка, дві прямі,
що перетинаються, два
центрально-симетричні кути, порожня множина точок, уся площина).
Якщо використати
заміну змінних: q=py-n w= kx-m,
тоді отримаємо
рівняння
a|q| + b|w|= c з
двома дійсними невідомими (q; w) .
Узагальнення видів графіків рівняння
a|py-n| +b|kx-m|= c, якщо не нульові парметри k та p |
||||||||
С<0
|
a>0
|
a<0
|
a=0
|
С=0
|
a>0
|
a<0
|
a=0
|
|
b>0
|
порожня
множина
|
два
кути
|
дві
прямі
|
b>0
|
одна
точка
|
дві
прямі
|
одна
пряма
|
|
b<0
|
два
кути
|
ромб
|
дві
прямі
|
b<0
|
дві
прямі
|
одна
точка
|
одна
пряма
|
|
b=0
|
дві
прямі
|
дві
прямі
|
порожня
множина
|
b=0
|
одна
пряма
|
одна
пряма
|
уся
площина
|
|
С>0
|
a>0
|
a<0
|
a=0
|
|||||
b>0
|
ромб
|
два
кути
|
дві
прямі
|
|||||
b<0
|
два
кути
|
порожня
множина
|
дві
прямі
|
|||||
b=0
|
дві
прямі
|
дві
прямі
|
порожня
множина
|
|||||
Випадок порожньої множини точок. Дане рівняння немає дійсні розв’язки, якщо виконуються
умови: 1) а<=0,
b<=0, c>0
або виконуються умови: 2)
1) а>=0,
b>=0, c<0.
Це слідує з того факту, що ліва та права частини рівняння мають різні знаки на
усій дійсній множині пар (х; у) . У цьому випадку графіку у даного рівняння не
існує(порожня множина точок площини), бо не існує пари чисел, які задовольняють
рівняння.
Випадок рівняння ромба: За одночасного виконання умов: {а>0; b>0; с>0, c/bk >0, c/pa > 0} або {а<0; b<0; с<0, c/bk >0, c/pa > 0} дане рівняння задовольняють безліч пар дійсних чисел, які
позначатимемо: (x1;y1) (x2;y2), (x3;y3), (x4;y4), відповідно до
чотирьох умов:
(x1;y1) = (x1; (-bkx1+c+bm+an)/ap), якщо {(x1;y1) | n/p<=y1<+oo; m/k<=x1<+oo}
(x2;y2) = (x2;
(bkx2+c-bm+an)/ap),
якщо {(x2;y2) | n/p<=y2<+oo; -oo<x2<m/k}
(x3;y3) = (x3; (-bkx3+c+bm-an)/(-ap)), якщо
{(x3;y3) | -oo<y3< n/p; m/k<=x3<+oo}
(x4;y4) =
( x4; (bkx4+c-bm-an)/(-ap)), якщо {(x4;y4) |
-oo<y4< n/p; -oo<x4<m/k}
Тоді графік такого рівняння описує фігура ромб:
·
з
центром в точці, що має координати: (m/k; n/p)
·
довжиною
горизонтальної півдіагоналлі c/bk >0
·
довжиною вертикальної півдіагоналлі
c/pa > 0
Випадок рівняння двох центральносиметричних кутів: за одночасного виконання умов: { аb<0; c<>0; c/bk >0, c/pa<0} або { аb<0; c<>0; c/bk<0, c/pa>0} дане рівняння задовольняють безліч пар дійсних чисел, які
позначатимемо: (x1;y1) (x2;y2), (x3;y3), (x4;y4), відповідно до
чотирьох умов:
(x1;y1) = (x1; (-bkx1+c+bm+an)/ap), якщо {(x1;y1) | n/p<=y1<+oo; m/k<=x1<+oo}
(x2;y2) = (x2;
(bkx2+c-bm+an)/ap),
якщо {(x2;y2) | n/p<=y2<+oo; -oo<x2<m/k}
(x3;y3) = (x3; (-bkx3+c+bm-an)/(-ap)), якщо
{(x3;y3) | -oo<y3< n/p; m/k<=x3<+oo}
(x4;y4) =
( x4; (bkx4+c-bm-an)/(-ap)), якщо {(x4;y4) |
-oo<y4< n/p; -oo<x4<m/k}
Тоді графік
такого рівняння описує фігура, що утворює два кути, які симетричні відносно центру симетрії, що має
координати: (m/k; n/p).
Якщо c/bk <=0 і c/pa >=0, тоді один кут
внутрішньою областю дивиться вгору, а
інший кут дивиться вниз і вершини
двох кутів розташовуються в відповідних точках: (m/k; c/pa+n/p), (m/k; -c/pa+n/p),
Якщо c/pa <=0
і c/bk >=0, один кут дивиться внутрішньою
областю ліворуч, а інший кут дивиться впаворуч, і вершини двох кутів розташовуються в
відповідних точках: (c/bk+m/k; n/p), (-c/bk+m/k; n/p).
Випадок рівняння однієї точки. Якщо {a>0; b>0; с=0} або {a<0; b<0; с=0} , то графік рівняння є однією точкою, яка має
координати: (m/k; n/p). Розв’язком
рівняння являється пара чисел: (m/k; n/p).
Випадок рівняння двох прямих, що перетинаються. Якщо
{a<0; b>0; с=0} або {a>0; b<0; с=0} , то графік рівняння є дві прямі, які
перетинаються в точці: (m/k; n/p).
Випадок рівняння площини. Якщо {a=0; b=0; с=0} , то графік рівняння є усі точки прямокутної системи координат.